Objetivos de aprendizaje

•          Racionalizar un denominador con un monomio que contiene una raíz cuadrada
•          Racionalizar un denominador que contiene dos términos

Introducción

Si bien los radicales siguen las mismas reglas que los enteros, a veces es difícil encontrar el valor de una expresión que contiene radicales. Por ejemplo, probablemente tienes una idea de cuánto es 

y, pero ¿y las cantidades 

y

? Estas son más difíciles de visualizar.

Dicho esto, algunas veces tendrás que trabajar con expresiones que contienen muchos radicales. Normalmente el valor de estas expresiones no es claro a simple vista. En casos donde tienes una fracción con un radical en el denominador, puedes usar una técnica llamada racionalizando un denominador para eliminar el radical. El objetivo de racionalizar un denominador es que sea más fácil de entender cuál es el valor de la cantidad al eliminar los radicales de los denominadores.

¿Qué es racionalizar un denominador?

La idea de racionalizar un denominador tiene sentido si consideras la definición de “racionalizar.” Recuerda que los números  

5y 0.75

y, y  son todos números racionales, cada uno puede expresarse como la razón de dos enteros (y  respectivamente).

 Algunos radicales son números irracionales porque no pueden representarse como la razón de dos enteros. Como resultado, el objetivo de racionalizar un denominador es cambiar la expresión de tal forma que el denominador se vuelve un número racional.

ejemplo 

Irracional		Racional
	=
	=

Ejemplo

Problema

Racionalizar el denominador.

El denominador de esta fracción es 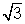. Para convertirlo a un número racional, multiplícalo por 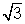, ya que .

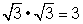Multiplica toda la fracción por un equivalente de 1, .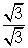

Usa la Propiedad Distributiva para multiplicar .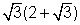

Simplifica los radicales, donde sea posible. .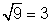

Respuesta